مارکس ورتهایمر (درگذشته به سال ۱۹۴۳) یکی از بنیانگذاران مکتب «گِشتالت» بود. (به طور خلاصه، گشتالتیها معتقدند باید به هر چیز به صورت کلی نگاه کرد). او در کتاب خود با عنوان «تفکر آفرینش» به موضوعی با عنوان «یادگیری از راه بینش» میپردازد و سعی میکند با یک مثال در حل مسائل ریاضی، منظور خود را بیان کند که من میخواهم در این مطلب آن مثال جالب را با جزئیات بیشتر توضیح دهم و همان نتیجه گشتالتیها را بگیرم:
روانشناسان گشتالت معتقدند روش حل مسأله مورد تأکید ورتهایمر که در بالا توضیح داده شد، راه حل اصیل و درست مسأله است که بر حفظ طوطیوار راهحلهای معمول برتری دارد. دانشآموزانی که به این روش یاد میگیرند، هم یادگیری آنها عمیقتر است و هم مطالب آموختهشده را دیرتر فراموش میکنند.

بینش یا Insight یعنی انسان به طور ناگهانی و از درون، به دلیل مسائل پی ببرد.
بعداً دیوید آزوبل (۱۹۶۸) در نظریه خود که مبتنی بر نظریه ورتهایمر است با عنوان «نظریه یادگیری معنیدار کلامی» (یا Meaningful Learning)، این ایده را بهتر و کاملتر بیان میکند؛ آزوبل معتقد است:
یادگیری معنیدار یعنی آن نوع یادگیری که در آن، یادگیرنده بتواند مطلبی را که میآموزد به مطالب آموختهشده قبلی ربط دهد.
اگر مطلب جدید، به هیچ وجه قابل ربط دادن به مطالب قبلاً آموخته شده نباشد، یادگیری آن مطلب معنیدار نخواهد بود و لازم است با تکرار و تمرین زیاد، به صورت طوطیوار آموخته شود.
و اینجاست که طبق نظریه آزوبل، پیشسازماندهندهها در آموزش بسیار اهمیت پیدا میکنند. به طور خودمانی، پیشسازماندهندهها آن چیزهایی هستند که دانشآموز باید قبل از یادگیری یک مفهوم جدید، آنها را یاد گرفته باشد؛ همان مفهوم «پیشنیاز» در دانشگاه و...
آزوبل گفته مشهوری دارد:
اگر قرار بود تمام مطالب روانشناسی پرورشی را تنها در یک اصل خلاصه کنم، آن اصل این است: «تنها عامل مهمی که برای یادگیری بیشترین تأثیر را دارد آموختههای قبلی یادگیرنده است». به این اصل تحقق بخشید و طبق آن آموزش دهید.
مثالی از یادگیری مبتنی بر بینش یا یادگیری معنیدار
برای اینکه بفهمید یادگیری معنیدار چقدر عمیق و جالب است، ابتدا به این سؤالات پاسخ دهید:
۱- آیا فرمول مساحت مربع را به خاطر دارید؟
۲- آیا فرمول مساحت مستطیل را به خاطر دارید؟
۳- آیا فرمول مساحت متوازی الاضلاع را به خاطر دارید؟
۴- آیا فرمول مساحت مثلث متساوی الاضلاع را به خاطر دارید؟
۵- آیا فرمول مساحت ذوزنقه را به خاطر دارید؟
اگر مدتی از دوران راهنمایی یا دبیرستان دور شده باشید، قول میدهم فرمول مساحت متوازی الاضلاع و ذوزنقه و حتی شاید مساحث مثلث را فراموش کرده باشید؛ چرا؟ چون فرمولی یاد گرفتهاید.
اما حالا بیایید به صورت معنیدار یاد بگیریم:
- مساحت مربع:
خوب، مساحت مربع را میتوان جزء علوم بدیهی دانست!

اگر ضلع مربع بالا ۱ متر باشد، طبیعتاً مساحت این کاشی (یا مثلاً موزاییک) ۱ در ۱ است؛ یعنی در حقیقت طول ضرب در عرض. (که البته طول و عرض یکسان است)
- مساحت مستطیل
احتمالاً میدانید که مساحت مستطیل هم همان طول ضرب در عرض است، اما چرا؟

با توجه به شکل بالا مشخص است، چون در حقیقت باید ببینیم برای کاشی کردن کف این اتاق چند تا کاشی نیاز داریم؟ که ضرب تعداد کاشیهای طول در عرض، تعداد کل یا همان مساحت را به دست میدهد؛ پس به این دلیل فرمول محاسبه مساحت مستطیل، عبارت است از:
طول x عرض
- مساحت متوازی الاضلاع
شاید با نگاه اول به متوازی الاضلاع نتوانید فرمول مساحت آن را به یاد بیاورید:

اما اگر من دو خطچین بکشم، شما با بینش و نسبت دادن به دانش قبلی خود میفهمید که متوازی اضلاع در حقیقت همان مستطیل است:
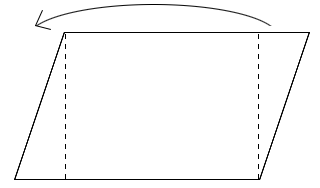
فقط کافیست آن تکه مثلث را از سمت راست بردارید و بگذارید سمت چپ. میبینید که این شکل همان مستطیل اولیه است! پس مساحت متوازی الاضلاع هم مانند همان مستطیل محاسبه میشود؛ فقط اینجا به جای طول میگوییم قاعده و به جای عرض میگوییم ارتفاع؛ پس:
قاعده x ارتفاع
- مساحت مثلث قائم الزوایه
فرمول مساحت این مثلث چه بود؟
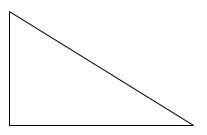
خوب، کافیست یک کپی از این مثلث بگیرید و کنار خودش قرار دهید:
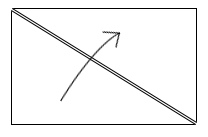
پس، این هم همان مستطیل خودمان است! (دانش قبلی) فقط باید یک تقسیم بر دو شود؛ مساحت مثلث از طریق همان طول ضرب در عرض محاسبه میشود؛ تقسیم بر ۲ ؛ که در ریاضی گفته میشود:
(قاعده x ارتفاع)
________
2
- مساحت مثلث متساوی الاضلاع یا متساوی الساقین:
فرمول مساحت این مثلث چه بود؟
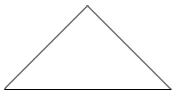
خوب، کافیست از آن هم یک کپی بگیرید و به طور برعکس کنار خودش قرار دهید:
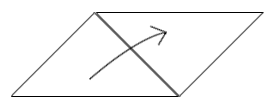
میبینید که یک متساوی الاضلاع تشکیل شد و از قبل میدانید که متساوی الاضلاع در حقیقت همان مستطیل است! پس مساحت این مثلث هم همان قاعده ضرب در ارتفاع است، فقط چون یک کپی گرفتهایم، باید یک تقسیم بر ۲ داشته باشیم؛ یعنی:
(قاعده x ارتفاع)
_________
2
- مساحت ذوزنقه
فرمول ذوزنقه را عمراً به خاطر بیاورید:

خوب، بیایید از آن هم یک کپی بگیریم و کنار خودش قرار دهیم:

باز هم یک متوازی الاضلاع تشکیل شد و متوازی الاضلاع همان مستطیل است! پس مساحت این هم همان طول ضرب در عرض یا قاعده ضرب در ارتفاع است؛ فقط باید دقت کنید که شکل را دو تا کردهایم و یک نکته دیگر اینکه: ارتفاع که همان ارتفاع قبلی است؛ اما به قاعده دقت کنید: قاعدهی متوازی اضلاعی که تشکیل شده، در حقیقت جمع قاعده بالا و پایین ذوزنقه است. پس فرمول مساحت ذوزنقه چه میشود؟
(قاعده بالا + قاعده پایین) x ارتفاع
________________
2
من فکر میکنم اگر ۳۰ سال بعد هم از شما بپرسند مساحت متساوی الاضلاع یا مثلث یا ذوزنقه چطور محاسبه میشود دیگر بدانید که با یک تغییر ساده در شکل، آن شکل تبدیل به دانش قبلی شما میشود که فرمولش جزء بدیهیات است!
مدرسین باید تلاش کنند هر مبحث جدید را به همین صورت به دانستههای قبلی دانشجو مرتبط سازند و تا جایی که ممکن است، حفظ طوطیوار را از آموزش حذف کنند.
موفق باشید؛
حمید رضا نیرومند


 English
English العربی
العربی Swedish
Swedish François
François









![[آی.جدول: اسکریپت ایجاد جدول آنلاین]](/img/blocks/ijadval.png)
![[مِلکا: سیستم مدیریت مشاور املاک]](/img/blocks/melka.png)
![[پارسخوان: نرم افزار خوانای متن فارسی]](/img/blocks/parskhan.png)
![[بوکفا ۲: سیستم مدیریت آنلاین کتابخانه]](/img/blocks/bookfa.png)
![[QuranPDF: قرآن پی.دی.اف]](/img/blocks/quran_pdf.png)
![[Robi: روبات روبی]](/img/blocks/robi.png)
![[هیسسس: سیستم هیسگوی خودکار: اولین سختافزار آفتابگردانی]](/img/blocks/hisss.png)
![[آی قصه!: نرم افزاری برای تقویت داستان سرایی کودکان]](/img/blocks/iqesseh.png)
![[دُر: نرمافزار کتابخوان تدریجی]](/img/blocks/dor.png)
![[Fonta: پژوهشی درباره فونت]](/img/blocks/fonta_book.png)
![[چگونه یک تجارت الکترونیک راهاندازی کنم]](/img/blocks/ecommerce_book.png)

![[بازی آنلاین نیکا]](/img/blocks/nika_ads.png)
 علی:
علی: